Hints On Solving Word Problems Or Applications Of Trigonometry:
- If no diagram is given, draw one yourself.
- Mark the right angles in the diagram.
- Show the sizes of the other angles and the lengths of any lines that are known
- Mark the angles or sides you have to calculate.
- Consider whether you need to create right triangles by drawing extra lines. For example, divide an isosceles triangle into two congruent right triangles.
- Decide whether you will need Pythagorean theorem, sine, cosine or tangent.
- Check that your answer is reasonable. For example, the hypotenuse is the longest side in a right triangle.
Example:
A ladder 5 m long, leaning against a vertical wall makes an angle of 65˚ with the ground.
a) How high on the wall does the ladder reach?
b) How far is the foot of the ladder from the wall?
c) What angle does the ladder make with the wall?
Solution: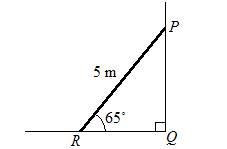
a) The height that the ladder reach is PQ![]()
PQ = sin 65˚ × 5 = 4.53 m
b) The distance of the foot of the ladder from the wall is RQ.![]()
RQ = cos 65˚ × 5 = 2.11 m
c) The angle that the ladder makes with the wall is angle P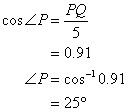
Leave a Reply