If we know the size of an angle, we can find the sin, cos and tan of the angle by using a scientific calculator. We can also use a calculator to find the inverse or reverse of this. If we know the sin, cos or tan of an angle, we can find the size of the angle.
If tan θ = x then tan -1 x = θ
If sin θ = x then sin -1 x = θ
If cos θ = x then cos -1 x = θ
Example:
Find the values of θ for the following (Give your answers in degrees and minutes):
a) tan θ = 2.53
b) sin θ = 0.456
c) cos θ = 0.6647
Solution:
a) Press

tan -1 2.53 = 68˚ 25 ’ 59.69 ” ( The ” symbol denotes seconds. There are 60 seconds in 1 minute.)
= 68˚ 26 ’ (to the nearest minute)
b) Press

sin -1 0.456 = 27˚ 7 ’ 45.46 ”
= 27˚ 8 ’ (to the nearest minute)
b) Press
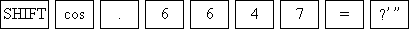
cos -1 0.6647 = 48˚ 20 ’ 26.47 ”
= 48˚ 20 ’ (to the nearest minute)
Example:
Calculate the angle x in the figure below. Give your answer correct to 4 decimal places.
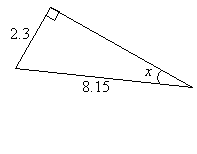
Solution:
sin x = ![]()
x = sin -1(2.3 ÷ 8.15)
= 16.3921˚
Leave a Reply