How to remember the signs of the trigonometric functions for the four quadrants?
We can use a mnemonic like CAST or** A**ll** S**tudents **T**ake** C**alculus to remember the signs in the 4 quadrants.
The following figure shows the signs of the trigonometric functions for the four quadrants. Scroll down the page for more examples and solutions. 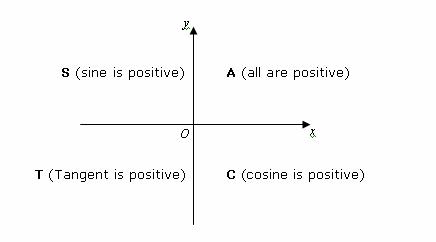
The trigonometric ratios for 0˚, 90˚, 180˚, 270˚ and 360˚ are shown below:
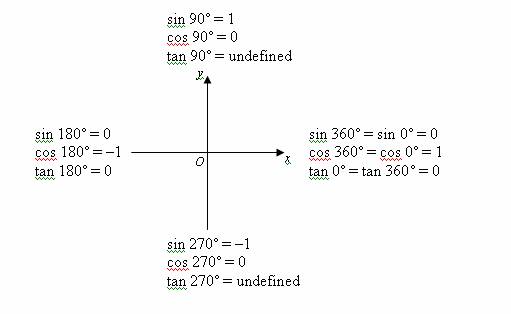
Take note of the signs of the trigonometric ratios in the following examples.
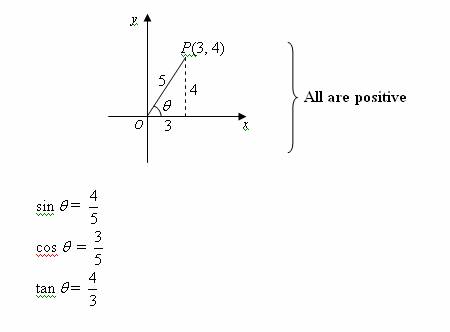
Quadrant 1 (0° < θ < 90°)
In the following diagram, θ is in the first quadrant.
Sine, cosine and tangent are all positive.
Quadrant II (90° < θ < 180°)
In the following diagram, θ is in the second quadrant.
The reference angle, α = 180° – θ
Sine is positive whereas cosine and tangent are negative.
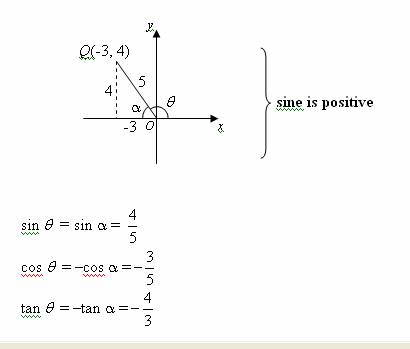
Quadrant III (180° < θ < 270°)
In the following diagram, θ is in the third quadrant.
The reference angle, α = θ – 180°
Tangent is positive whereas sine and cosine are negative.
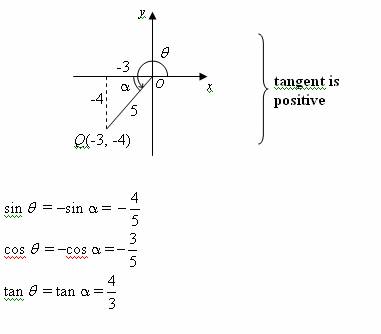
Quadrant IV (270° < θ < 360°)
In the following diagram, * θ* is in the fourth quadrant.
The reference angle, α = 360° – θ
Cosine is positive whereas sine and tangent are negative.
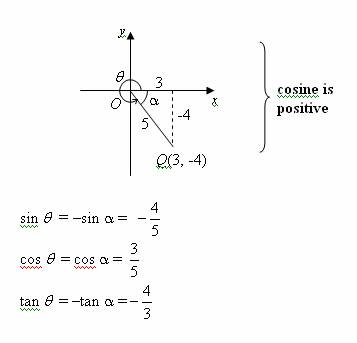
Example:
Determine the sign of each of the following values.
a) cos 121°
b) tan 220°
Solution:
a) cos 121° is in quadrant II (90° < 121° < 180°)
In quadrant II, only sine is positive, so cos 121° is negative.
b) tan 220° is in quadrant III (180° < 220° < 270°)
In quadrant III, tangent is positive, so tan 220° is positive.
Leave a Reply