Intro to Linear Equations

A linear equation is an equation that describes a straight line on a graph. You can remember this by the “line” part of the name linear equation.

Standard Form

Linear equations have a standard form that looks like this:

Ax + By = C

Where A, B, and C are coefficients (numbers) while x and y are variables.

You can think of the x and y variables as points on a graph. Example linear equations: You can plug numbers into A, B, and C of the above standard form to make linear equations:

2x + 3y = 7

x + 7y = 12

3x – y = 1

Linear Equations Represent Lines

At first it may seem strange that an equation represents a line on a graph. To make a line you need two points. Then you can draw a line through those two points.

The x and y variables in the linear equation represent the x and y coordinates on a graph. If you plug in a number for x, you can calculate the corresponding number for y. Those two numbers show a point on a graph. If you keep plugging in numbers for x and y in a linear equation, you will find that all the points together make a straight line.

Graphing a Linear Equation

In order to graph a linear equation you can put in numbers for x and y into the equation and plot the points on a graph. One way to do this is to use the “intercept” points. The intercept points are when x = 0 or y = 0. Here are some steps to follow:

• Plug x = 0 into the equation and solve for y
• Plot the point (0,y) on the y-axis
• Plug y = 0 into the equation and solve for x
• Plot the point (x,0) on the x-axis
• Draw a straight line between the two points

You can check your answers by trying other numbers in the equation. Try x = 1. Solve for y. Then make sure that that point is on your line.

Example Problem:

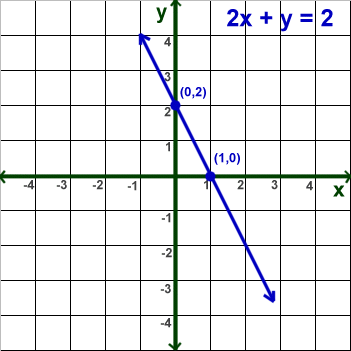
Graph the linear equation: 2x + y = 2

Step 1:

Plug in x = 0 and solve for y.

2 (0) + y = 2 y = 2

Step 2:

Plug in y = 0 and solve for x. 2x + 0 = 2 2x = 2 x = 1

Step 3:

Graph the x and y intercept points (0, 2) and (1,0)

Step 4:

Draw a straight line through the two points

Step 5:

Check the answer.

We will put in 2 for x and solve:

2(2) + y = 2

4 + y = 2

y = 2 – 4

y=-2

Is the point (2,-2) on the line?

You can try some other points to double check as well.

Example 2:

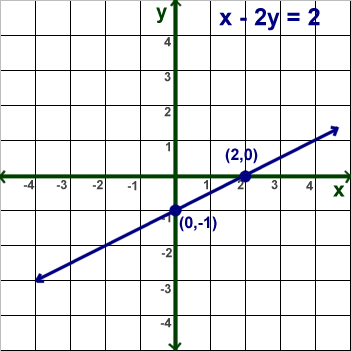
Graph the linear equation x – 2y = 2

Step 1:

x = 0 0 – 2y = 2 y = -1

Step 2:

y = 0 x – 2(0) = 2 x = 2

Step 3:

Graph the x and y points (0, -1) and (2,0)

Step 4:

Draw a line through the two points

Step 5:

Check your answer.

Let’s try x = 4

4 – 2y = 2

-2y = 2 – 4

-2y = -2

2y = 2

y = 1

Is the point (4,1) on the graph?