Law of Sines

In these lessons, we will learn

• the Law of Sines,
• how to use the Law of Sines when given two angles and one side,
• how to use the Law of Sines when given two sides and a non-included angle,
• about the ambiguous case when using the Law of Sines,
• about the “no solutions” case when using the Law of Sines,
• the proof for the Law of Sines,
• how to solve applications or word problems using the Law of Sines.

Law of Sines

The Law of Sines states that:
In any given triangle, the ratio of the length of a side and the sine of the angle opposite that side is a constant.

The following figure shows the Law of Sines for the triangle ABC

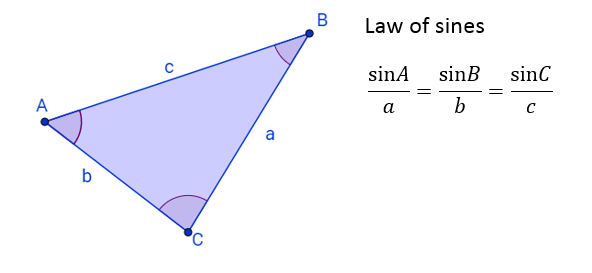
The law of sines states that

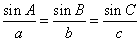
We can also write the law of sines or sine rule as:

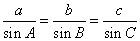
The Law of Sines is also known as the sine rule, sine law, or sine formula. It is valid for all types of triangles: right, acute or obtuse triangles.

The Law of Sines can be used to compute the remaining sides of a triangle when two angles and a side are known (AAS or ASA) or when we are given two sides and a non-enclosed angle (SSA).

We can use the Law of Sines when solving triangles. Solving a triangle means to find the unknown lengths and angles of the triangle. If we are given two sides and an included angle (SAS) or three sides (SSS) we will use the Law of Cosines to solve the triangle.