The main functions in trigonometry are Sine, Cosine and Tangent
They are simply one side of a right-angled triangle divided by another.
For any angle “θ“:

(Sine, Cosine and Tangent are often abbreviated to sin, cos and tan.)
Example: What is the sine of 35°?
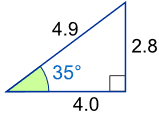
Using this triangle (lengths are only to one decimal place):
sin(35°) = OppositeHypotenuse = 2.84.9 = 0.57…
The triangle could be larger, smaller or turned around, but that angle will always have that ratio.
Calculators have sin, cos and tan to help us, so let’s see how to use them:
Example: How Tall is The Tree?
We can’t reach the top of the tree, so we walk away and measure an angle (using a protractor) and distance (using a laser):
- We know the Hypotenuse
- And we want to know the Opposite
Sine is the ratio of Opposite / Hypotenuse:
sin(45°) = OppositeHypotenuse

Get a calculator, type in “45”, then the “sin” key:
sin(45°) = 0.7071…
What does the 0.7071… mean? It is the ratio of the side lengths, so the Opposite is about 0.7071 times as long as the Hypotenuse.
We can now put 0.7071… in place of sin(45°):
0.7071… = OppositeHypotenuse
And we also know the hypotenuse is 20:
0.7071… = Opposite20
To solve, first multiply both sides by 20:
20 × 0.7071… = Opposite
Finally:
Opposite = 14.14m (to 2 decimals)When you gain more experience you can do it quickly like this:

Example: How Tall is The Tree?
Start with:sin(45°) = OppositeHypotenuse
We know:0.7071… = Opposite20
Swap sides:Opposite20 = 0.7071…
Multiply both sides by 20:Opposite = 0.7071… × 20
Calculate:Opposite = 14.14
(to 2 decimals)
The tree is 14.14m tall
Leave a Reply